Theoyu

『南京大学-软件分析』课程笔记

  • Theoyu
  • Mar 20, 2022

『 无论你是玩游戏多，还是成绩不太好，觉得自己没有别人毕业有优势，这都是因为浮躁、去比较产生的事情。这门课，老师希望你重新的审视自己，不断地认识自己、挖掘自己，看看真的什么东西能让你你快乐起来，什么东西能让你花时间去搞。哪怕你以后只是开了一家奶茶店，哪怕是一个和计算机毫无相关的行业，也希望你能从这么课中清楚的认识到自己喜欢的是什么，你不是没有别人优秀，你只是选择了你喜欢的事情。 』

去年5月因为大创零零散散看过，最近重新拾起来，第一节课还是被感动到了。

课程介绍

为什么我们需要静态分析

image-20220310205025687

  • 程序可靠性

    空指针引用、内存泄漏…

  • 程序安全性

    信息泄漏、注入攻击…

  • 编译优化

    死代码消除、代码移动(比如在循环里定义不会改变的值，可以把初始化放在循环外面)

  • 理解程序

    idea自动提示、分析结构…

Sound & Complete

程序分析不存在 exact answer

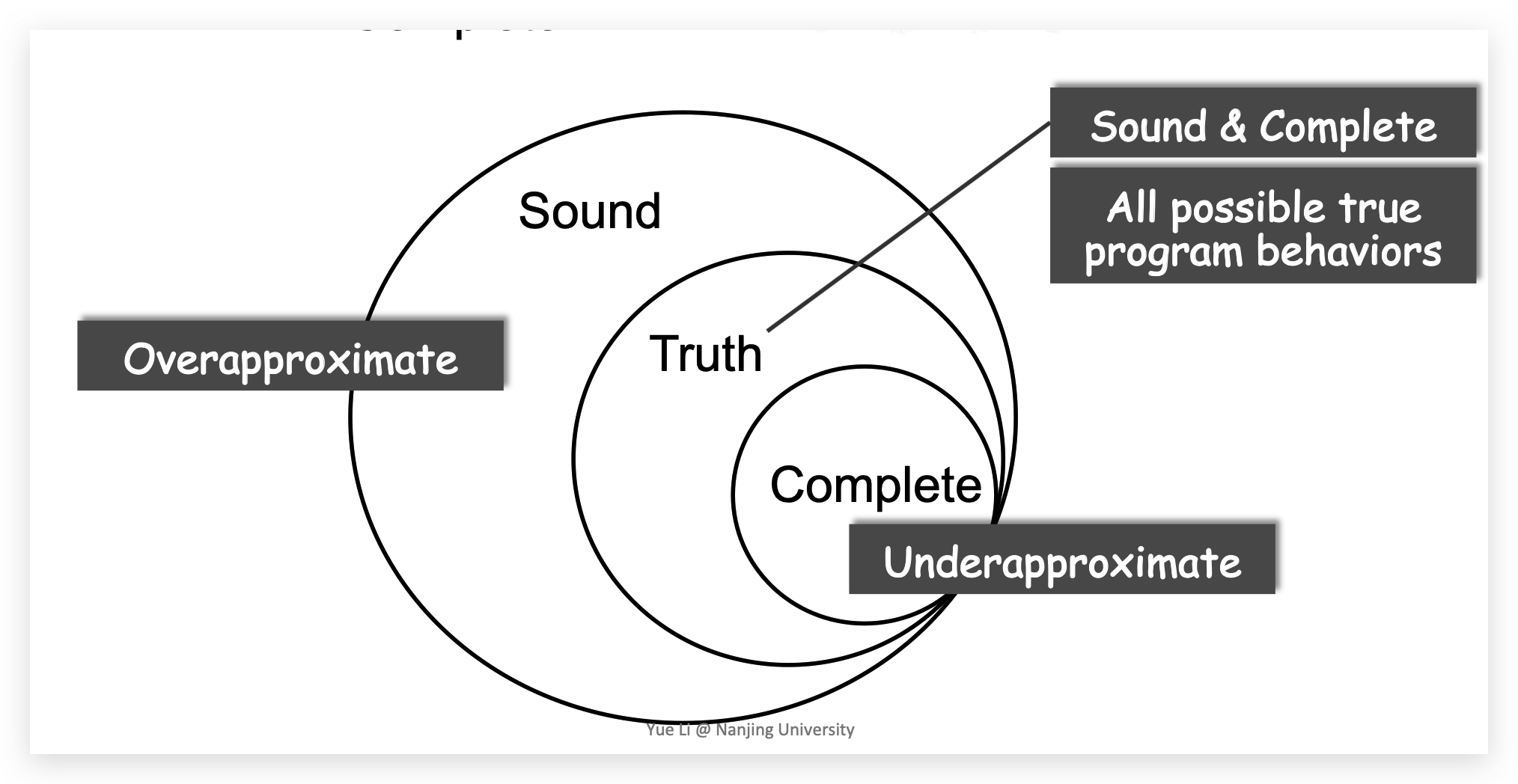
image-20220310222205046

Sound > Truth> Complete

如果Truth是10个漏洞，那么Sound可以有100个、1000个，是包含关系。

Comlete中检测出来的，都在Truth中，是子集关系。

  • 妥协 soundness -> 漏报 False Negatives 假阴性
  • 妥协 completeness -> 误报 False Positives 假阳性

注意这里『妥协』的概念，不然很容易弄反。

妥协 soundness，不是倾向于 Sound，而是相反不接收 Sound，也就是把Sound范围缩小到Complete，造成了漏报。

学术界的东西就是绕一些

准则：宁可误报不能漏报，妥协 completeness，保证soundness。

确保soundness的基础上，在精度和速度上作出权衡。

Intermediate Representation

Compilers and Static Analyzers

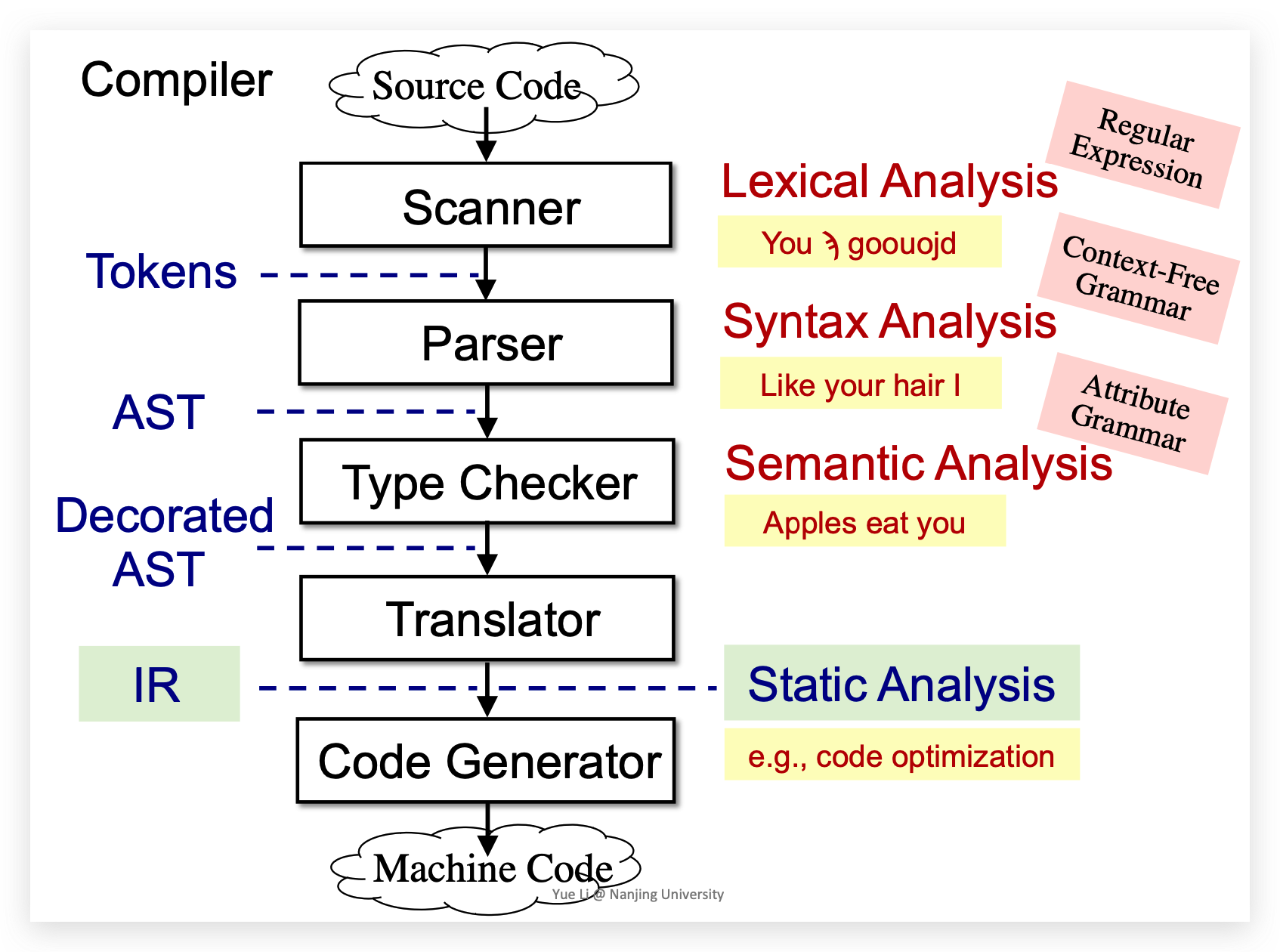
image-20220311102630000

编译器将源代码（Source code） 转换为机器代码（Machine Code）。其中的流程框架是：

  1. 词法分析器（Scanner），结合正则表达式，通过词法分析（Lexical Analysis）将 source code 翻译为 token。
  2. 语法分析器（Parser），结合上下文无关文法（Context-Free Grammar），通过语法分析（Syntax Analysis），将 token 解析为抽象语法树（Abstract Syntax Tree, AST）
  3. 语义分析器（Type Checker），结合属性文法（Attribute Grammar），通过语义分析（Semantic Analysis），将 AST 解析为 decorated AST 🎄
  4. Translator，将 decorated AST 翻译为生成三地址码这样的中间表示形式（Intermediate Representation, IR），并基于 IR 做静态分析（例如代码优化这样的工作），IR之前的部分我们称为前端，IR之后的部分称为后端。
  5. Code Generator，将 IR 转换为机器代码。

几个问题：

  1. 语法分析为什么是Context-Free Grammar？

    现在的编程语言完全足够，context-Sensitive Grammar更适合分析人讲的语言(NLP、ChatGPT)

  2. 为什么不直接拿Source code做静态分析，而是要经过到IR的这一系列步骤？

    分析代码漏洞，这是 non-trivial 的事情，做non-trivial 之前 应该把 trivial 的部分交给各种分析器去做。

AST vs. IR

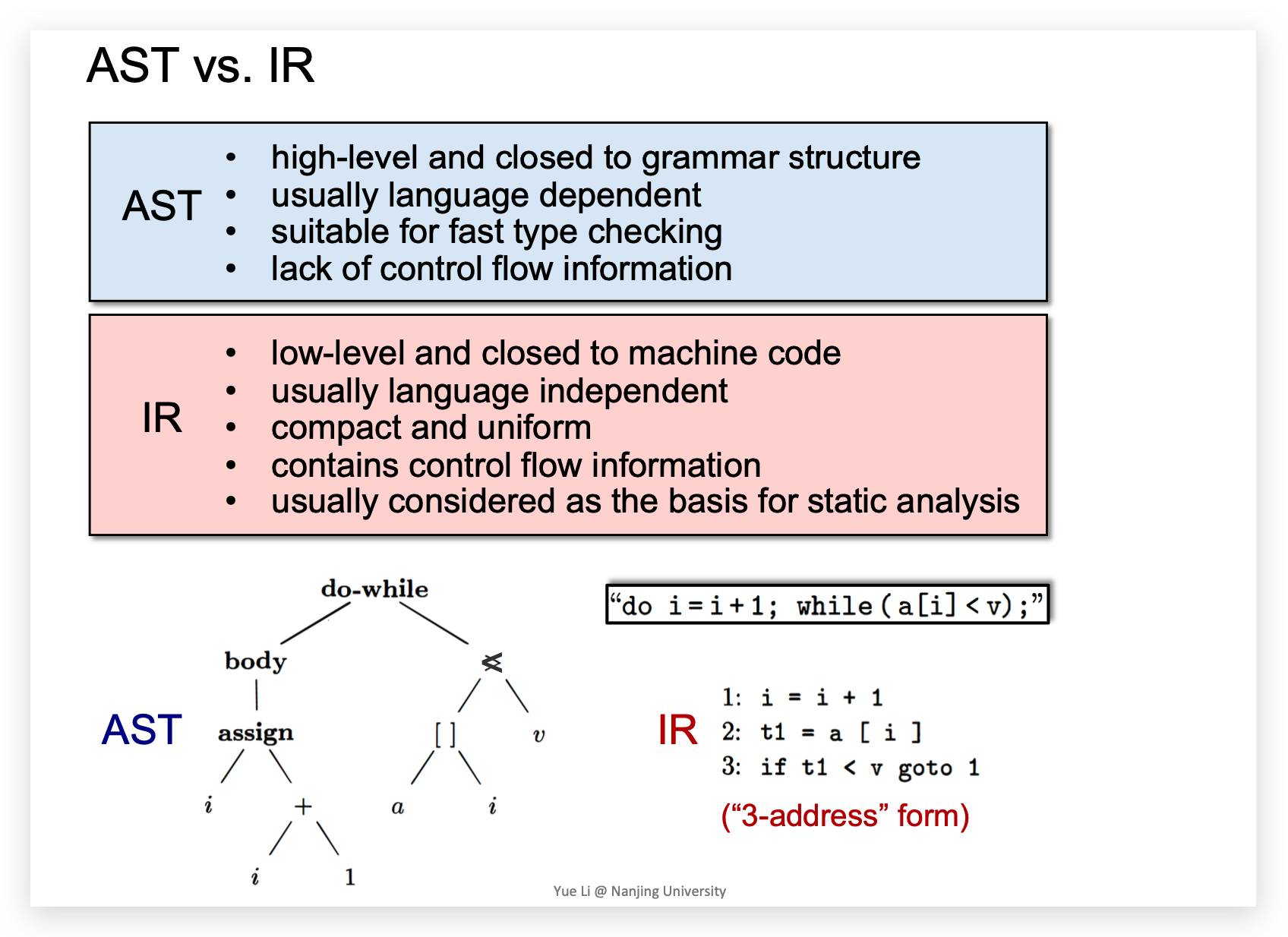
image-20220311121248887

  • AST ：高级，更接近于语法结构，依赖于语言种类，适用于快速类型检查，缺少控制流信息。

  • IR：低级，更接近于机器码，不依赖语言种类，压缩且简洁，包含控制流信息。是静态分析的基础。

IR: Three-Address Code

三地址码（3-Address Code）通常没有统一的格式。在每个指令的右边至多有一个操作符。

a+b+3 ==> t1=a+b
          t2=t1+3

三地址码为什么叫做三地址码呢？因为每条 3AC 至多有三个地址。而一个「地址」可以是：

  • 名称 Name: a, b
  • 常量 Constant: 3
  • 编译器生成的临时变量 Compiler-generated Temporary: t1, t2

常见的 3AC 包括：

  • $z=x\text{ }bop\text{ }y$ ：双目运算符并赋值，bop = binary operator
  • $x=uop\text{ }y$ ：单目运算符并，unary operator
  • $x=y$ ：直接赋值
  • $goto\ L$ ：无条件跳转，L = label
  • $if\text{ }x\text{ }goto\text{ }L$：条件跳转
  • $if\text{ }x\text{ }rop\text{ }y\text{ }goto\text{ }L$：包含运算关系的跳转，rop = relational operator

Soot and Its IR: Jimple

做到Assignments再记录

Static Single Assignment

静态单赋值（SSA），就是让每次对变量x赋值都重新使用一个新的变量xi，并在后续使用中选择最新的变量。

3AC        | SSA
p = a + b    p1 = a + b
q = p - c    q1 = p1 - c
p = q * d    p2 = q1 * d
q = p + q    q2 = p2 + q1

但这样如果多个控制流汇聚到一个块，会导致多个变量备选的问题：

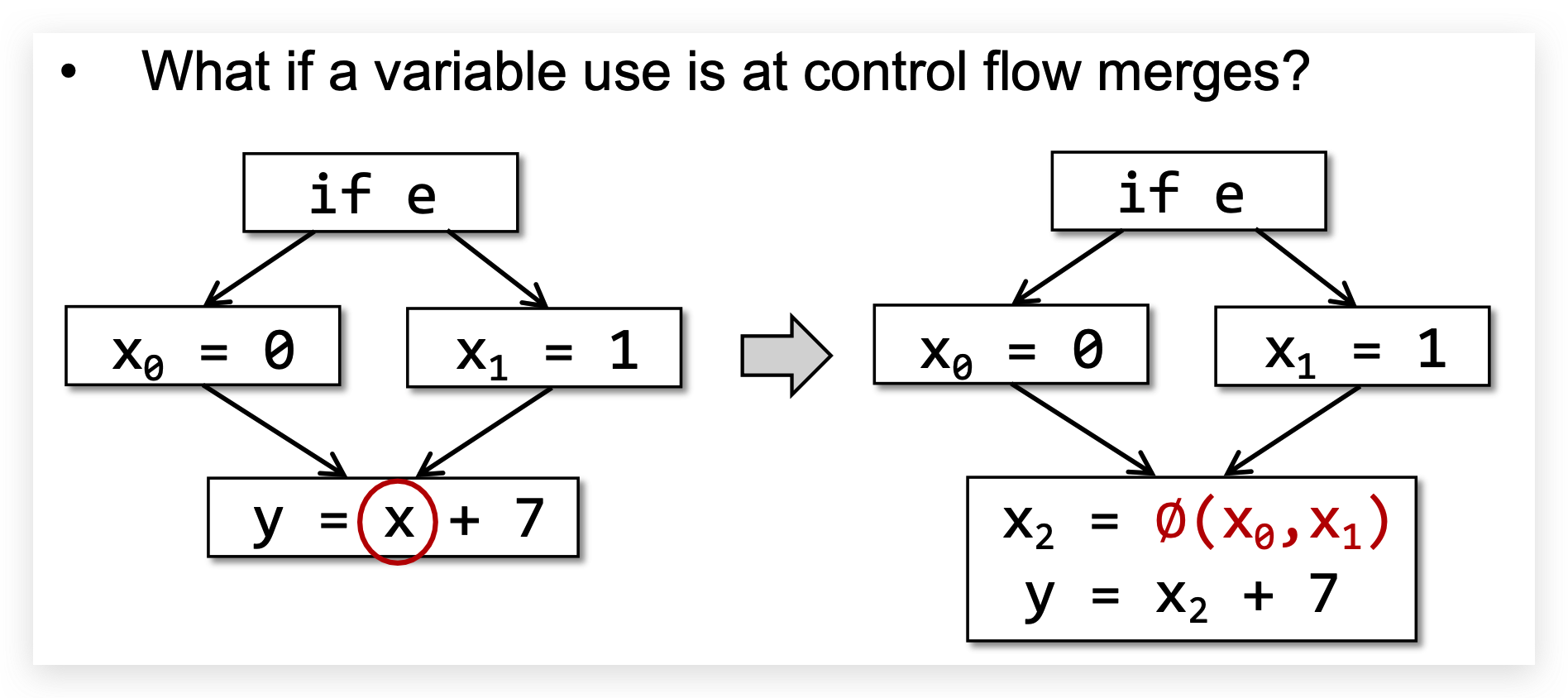
image-20220312154526879

解决：使用合并操作符$\phi$（phi-function），根据控制流的信息确定使用哪个变量

SSA优势：

  • flow-insensitive analysis精度更准确
  • 容易做优化算法

劣势：

  • 引入大量变量
  • 编译时有性能问题

Basic Blocks & Control Flow Graphs

控制流分析（Control Flow Analysis）通常指的是构建控制流图（Control Flow Graph, CFG），并以 CFG 作为基础结构进行静态分析的过程。

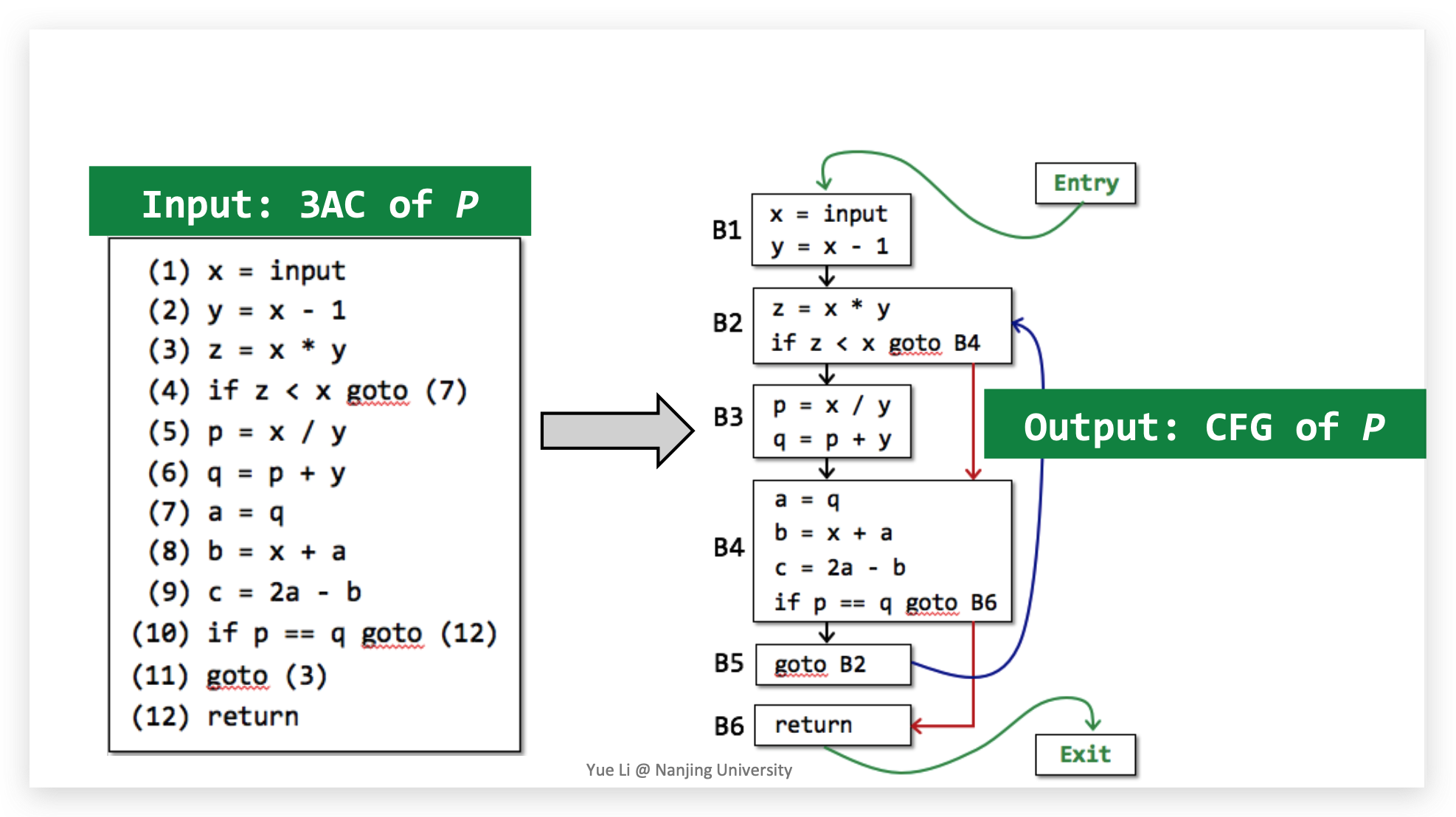
image-20220312171312499

The node in CFG can be an individual 3-address instruction, or (usually) a Basic Block (BB)

CFG的节点可以是单独的一条 3AC，但更常见的是一个基本块（Basic Block）。

BB的定义：只有唯一一个入口和唯一一个出口的最长3AC连续序列。

如果把连续的 3AC 识别为一个个BB：

  1. 找到所有 BB 的 leader(入口)：
    • 第一条指令就是一个 leader
    • 跳转指令跳转的目标指令是一个 leader（反证法，不然不满足唯一入口）
    • 跳转指令的下一条指令是一个leader（反证法，不然不满足唯一出口）
  2. 一个基本块就是一个 leader 及其后续直到下一个 leader 前的所有指令。

image-20220312173836125

除了基本块，CFG 中还会有块到块的边。块 A 和块 B 之间有一条边，当且仅当：

  • A 的末尾有一条指向了 B 开头的跳转指令。

  • A 的末尾紧接着 B 的开头，且 A 的末尾不是一条无条件跳转指令。

这样我们就完成了从3AC到CFG的转化。

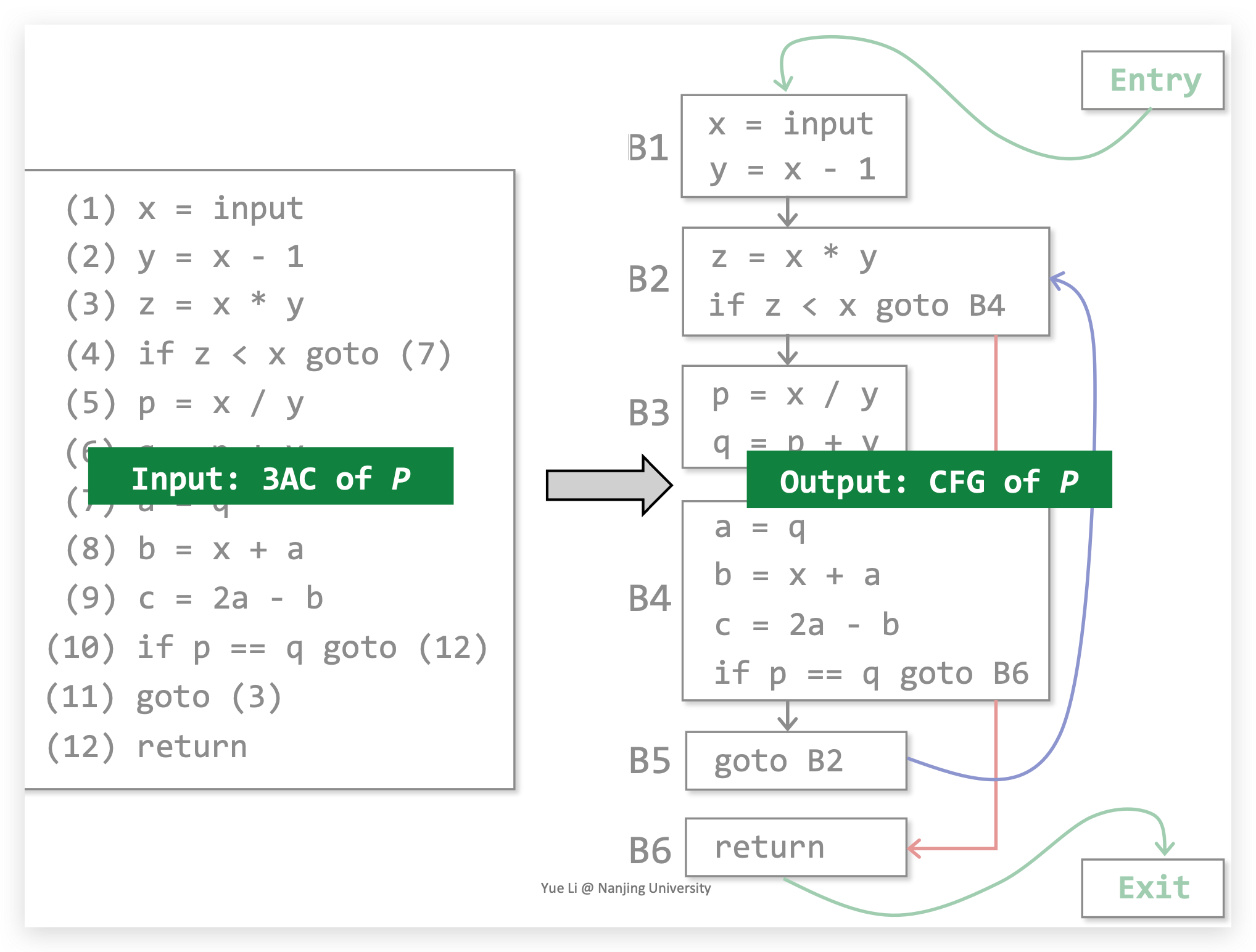
image-20220312174157931

Data Flow Analysis

Reaching Definitions Analysis

image-20230311183233545

定义：

  • 假如 p 处给 v 一个定义（赋值）d，从 p 到 q 此路径上没有 v 的其他定义，则称 v 的定值 d 到达（reaches）q。

  • 如果这条路径上存在对 v 的重新定义，则称 x 的定值 d 被 killed 。

对于一条赋值语句D: v = x op y，该语句生成了 v 的一个定值 D，并杀死程序中其它对变量 v 定义的定值。

应用：检测未定义变量使用：

  1. 在 CFG 中给每一个变量引入一个 dummy 定值。

  2. 当程序出口时该变量未被 killed，则我们可以认为该变量未被定义。

Transfer Function： \(\mathrm{OUT}[B]=gen_{B} \cup\left(\mathrm{IN}[B]-k i l l_{B}\right)\)

基本块 B 的输出 = B 内的所有变量 v 的定义（赋值/修改）语句 $\cup$ （基本块 B 的输入- 程序中其它所有定义 v 的地方）。本质就是本块与前驱修改变量的语句 作用之和（去掉前驱中已经定义的语句）。

Control-flow Handing： \(\mathrm{IN}[B]=\bigcup_{P \text { a predecessor of } B} OUT [P]\)

基本块 B 的输入 = 基本块 B 所有前驱块 P 的输出的并集。

这种数据流适合做 Forward Analysis

算法：

image-20230312183600205

Demo：

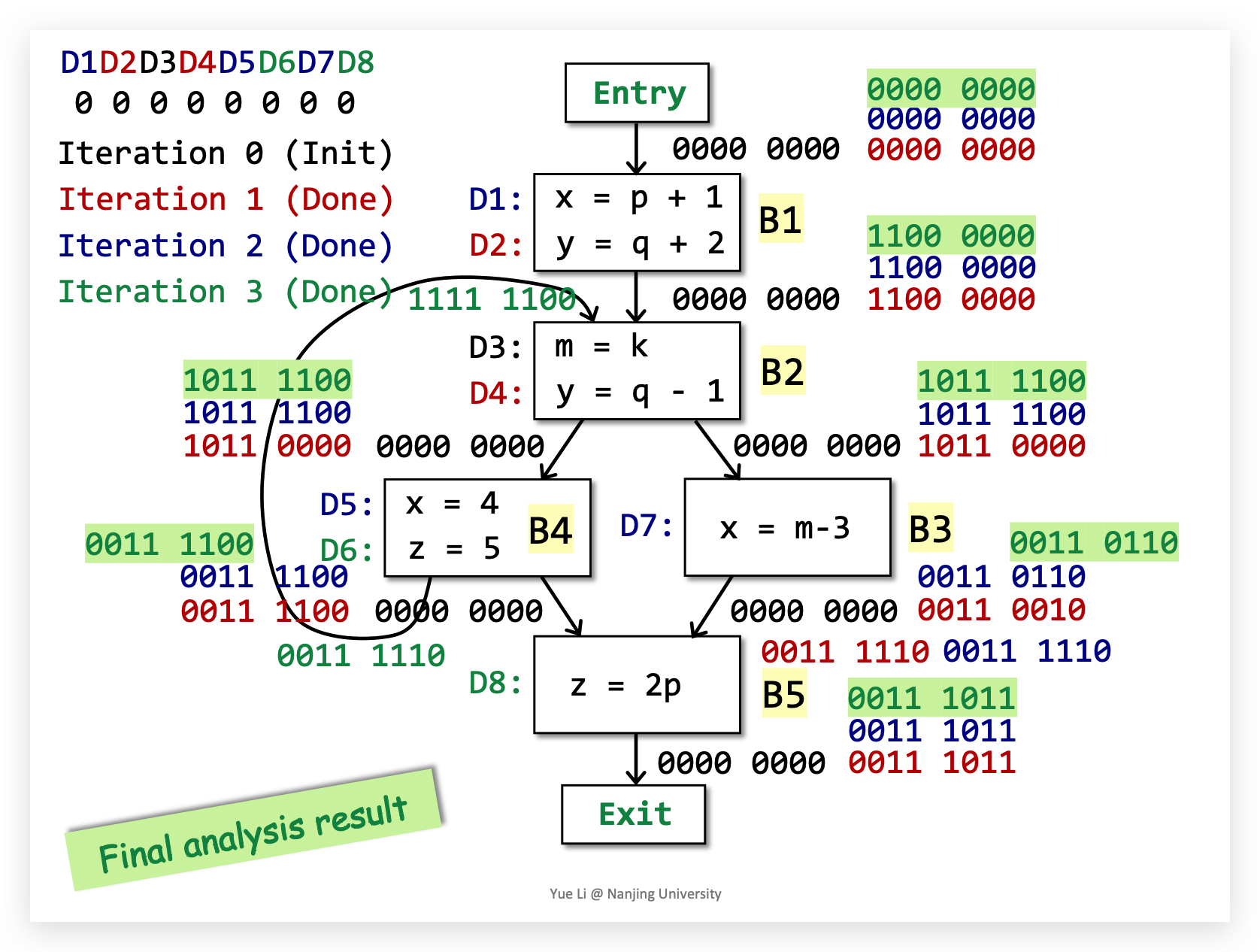
image-20230312183724251

Live Variables Analysis

image-20230319145635900

定义：

  • 在 CFG 语句 p 上定义的变量 v ，如果从 p 到 exit 上变量 v 被使用，则称 v 在 p 上是活跃变量。
  • 其中有一个隐含条件为 v 在使用前不能被重定义。

应用：寄存器分配：

  • 寄存器满了需要替换不会被使用的变量。

Control-flow Handing： \(\mathrm{OUT}[\mathrm{B}]=\bigcup_{S \text{ a successor of B}} {\mathrm{IN}[\mathrm{S}]}\)

基本块 B 的输出 = 所有 B 的后驱块 S 输入的并集

这种数据流适合做 Backward Analysis

Transfer Function： \(\mathrm{IN}[B]=use_{B} \cup\left(\mathrm{OUT}[B]-def_{B}\right)\)

基本块 B 的输入 = B 中（重定义前）被使用的变量 $\cup$ （ B的输出 -B 中重定义的变量）

算法：

image-20230319173519331

demo：

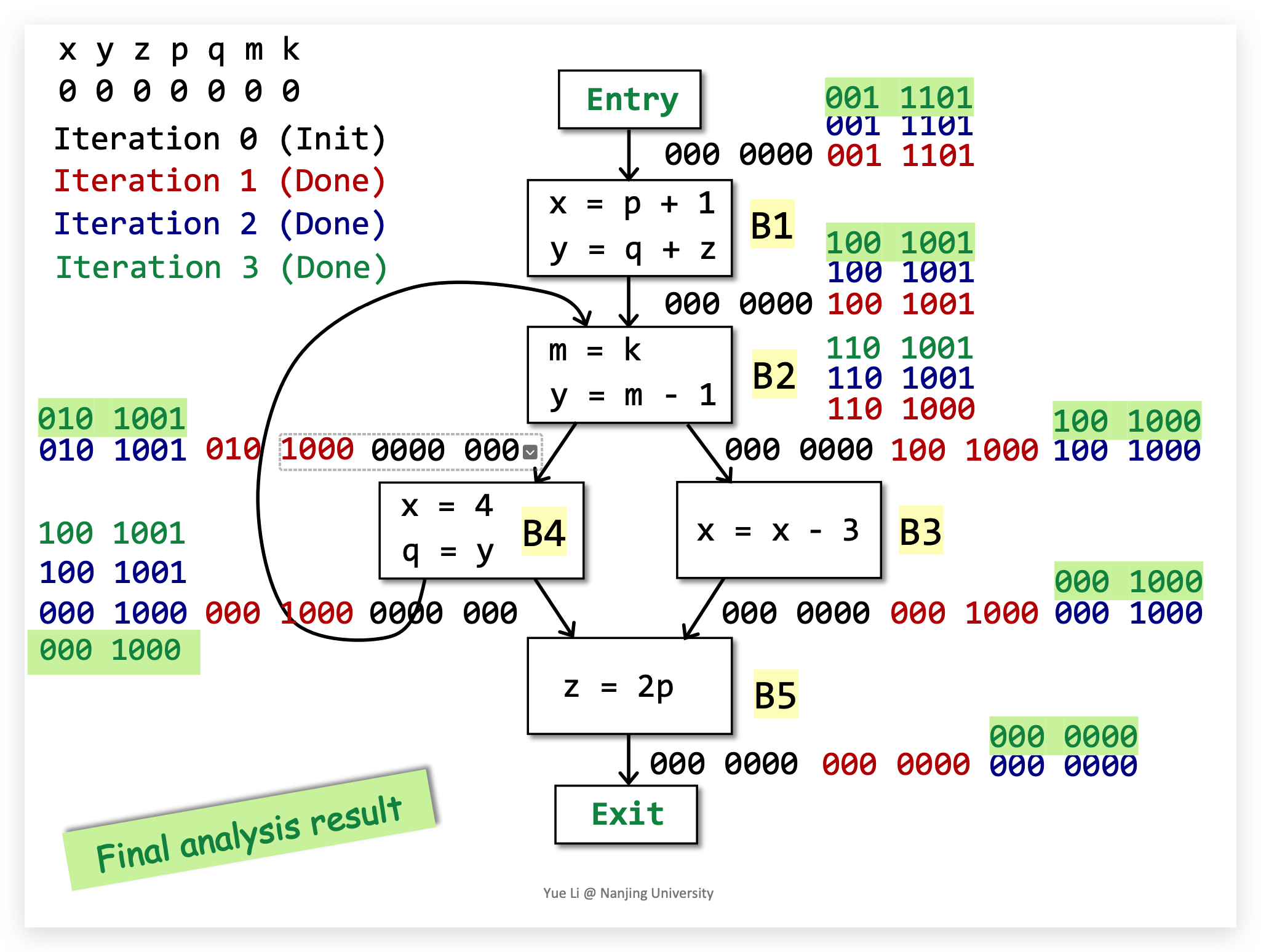
image-20230319175541740

Available Expression Analysis

image-20230325154715545

定义：

  • 表达式 $x\ op\ y$ 在 p 点为 available 当且仅当
    1. 从 entry 到 p 点的每一条路径都经过了表达式
    2. 每条路径经过表达式后，不能再有对 x 或 y 的重新赋值

应用：寄存器分配：

  • 用于优化，检测全局公共子表达式

Control-flow Handing： \(\mathrm{IN}[B]=\bigcap_{P a \text { predecessor of } B} OUT [P]\)

Forward and Must Analysis

Transfer Function：

\[\mathrm{OUT}[B]=gen_{B} \cup\left(\mathrm{IN}[B]-kill_{B}\right)\]

$kill_{B}$ 指基本块 B 中部分表达式的变量被重新赋值

算法：

image-20230325160416067

因为 Must Analysis 是做交集运算，所以 BB的初始化为全集

Demo：

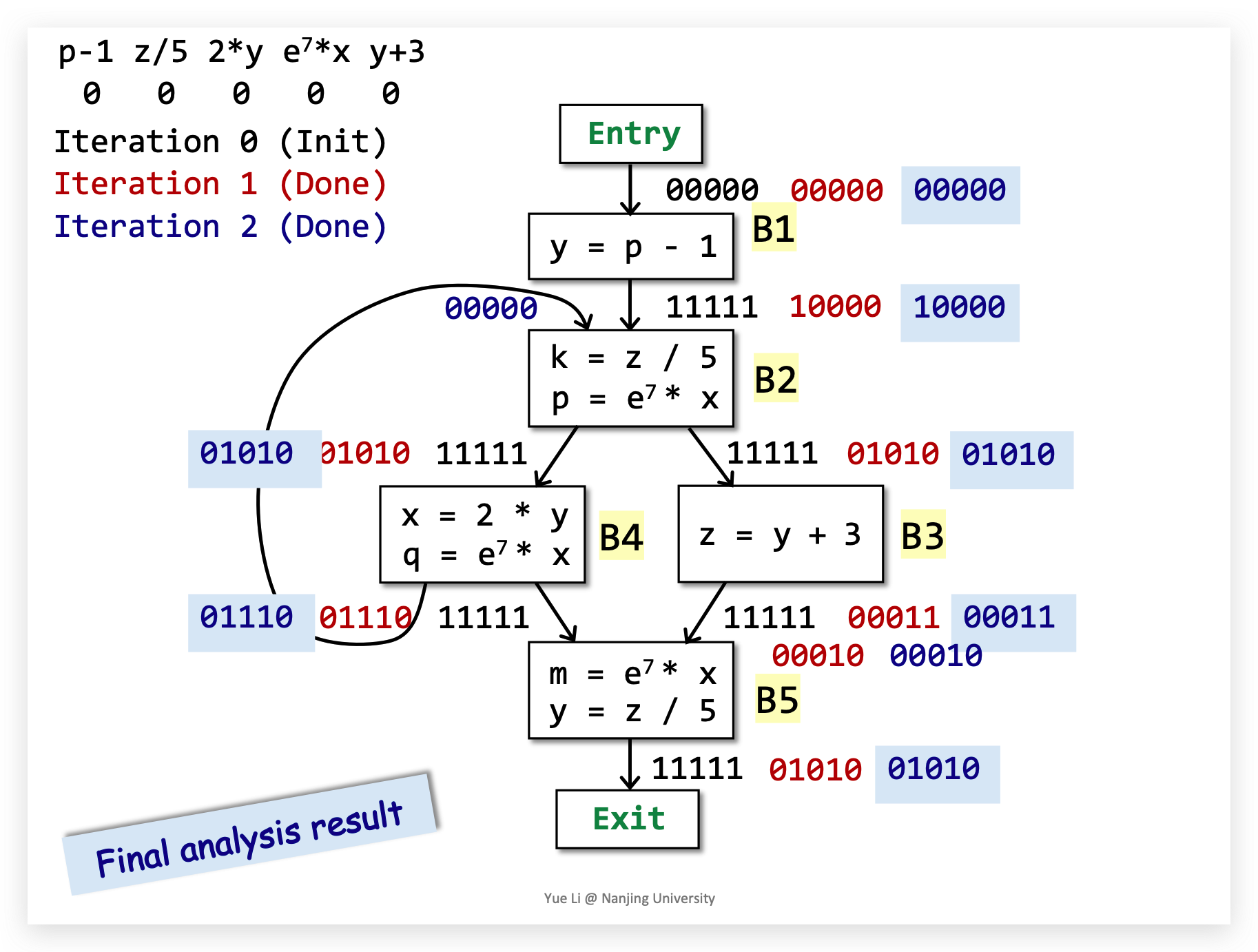
image-20230325160632224

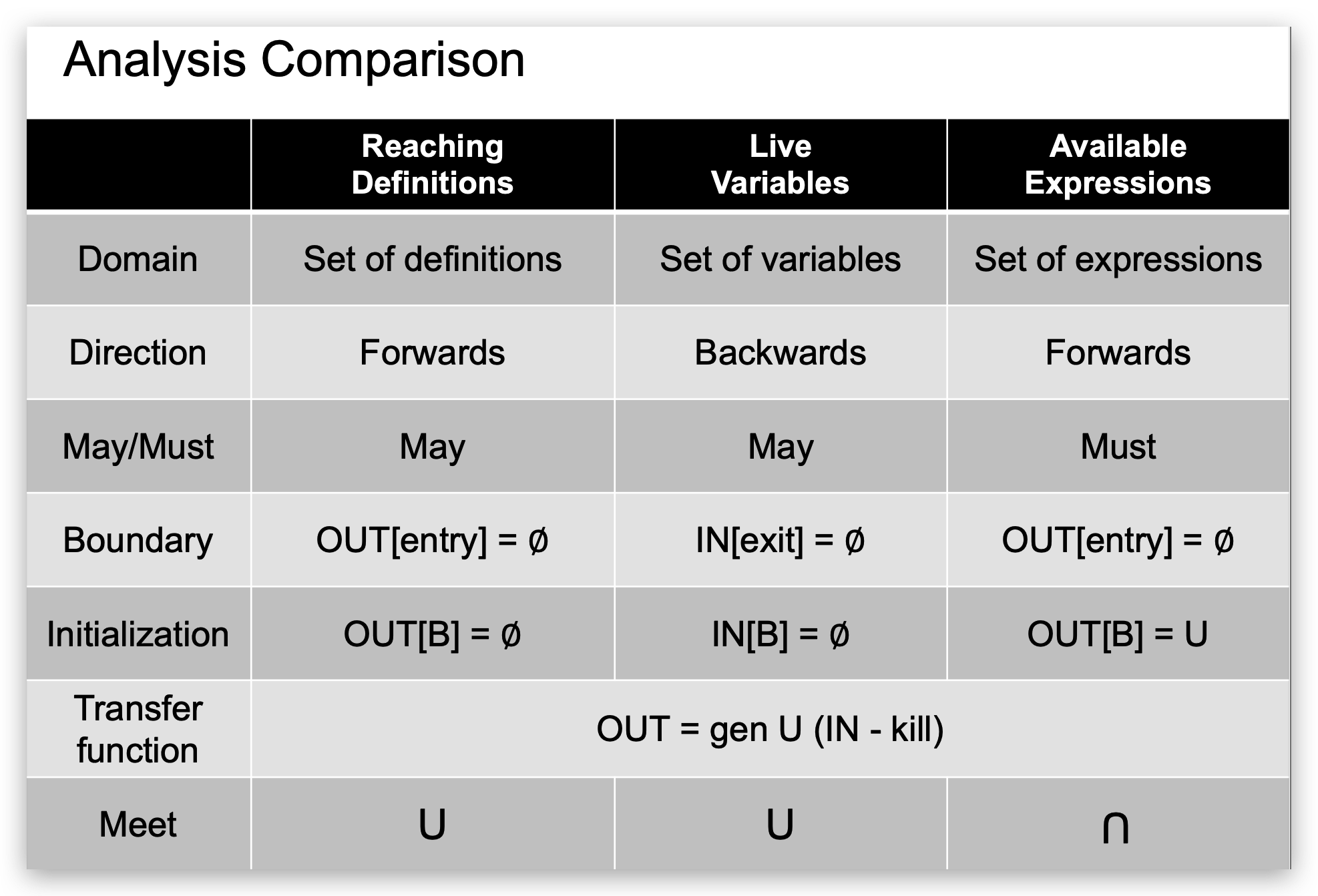
Analysis Comparison

image-20230325160902024

Search